엑셀 해찾기(Solver)에 대한 설명자료

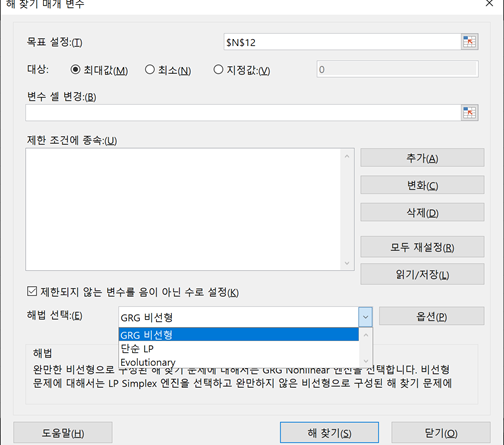
엑셀의 해찾기는 엑셀 2010에서 크게 기능이 향상되었습니다. 가장 크게 바뀐 점은 ‘해법 선택’ 드롭다운에서 해법을 선택할 수 있다는 점입니다. 여러분이 최적화하는 문제에 따라 적절한 해법 엔진을 선택할 수 있습니다. 다음과 같은 옵션이 있습니다.

• 단순 LP(Simplex LP) 엔진

: 선형 최적화 문제에 시용합니다. 선형 최적화 문제는 (변수 셀) * (상수) 항을 더해서 목표 셀과 제한 조건을 만들게 됩니다. 대부분 최적값을 찾고자 하는 모델은 비선형입니다.

• GRG(Generalized Reduced Gradient) 비선형 엔진

: 목표 셀과 제한 조건의 일부가 모두 비선형 혹은 목표 셀이나 제한 조건의 일부가 비선형인 최적화 문제를 풀기 위해 사용합니다. 계산할 때는 변수 셀을 곱하거나 나누는 등의 단순 계산 혹은 변수 셀을 거듭 제곱에 사용하거나, 지수 함수나 삼각 함수 등에 사용하는 것을 포함합니다. GRG 엔진을 사용하면 옵션에서 ‘Multistart’ 옵션을 사용할 수 있는데 이 옵션을 사용하면 이전 엑셀 버전에서 오답을 내던 문제들을 푸는데 제대로 사용할 수 있습니다. 실제로는 Multistart 옵션을 많이 사용할 것입니다.

• Evolutionary 엔진

: 목표 셀과 제한 조건 혹은 목표 셀이나 제한 조건에 변수 셀을 참조하는 완만하지 않은 비선형 함수가 들어있을 때 사용합니다. 예를 들어 여러분의 목표 셀이나 제한 조건에 변수 셀을 참조하는 IF, SUMIF, COUNTIF, SUMIFS, COUNTIFS, AVERAGEIF, AVERAGEIFS, ABS, MAX, MIN 등의 함수가 들어있으면 최적화된 답을 찾아내는데 이 Evolutionary 엔진이 최선의 선택일 것입니다. 많은 영역에서 Evolutionary 엔진 또한 많이 사용합니다.

목표 셀, 변수 셀, 제한 조건을 입력하고 나면 해찾기 프로그램은 무엇을 수행할까요? 만약 변수 셀이 제한 조건을 만족한다면 변수 셀은 기능한 해법이 될 수 있습니다. 그리고 해찾기는 이런 가능한 해법들 중에서 가장 적절한 해법의 집합을 찾습니다(이 값들을 최적값이라고 한다). 이 값은 목표셀에 대한 최선의 값입니다(극대화시킬 때는 가장 크게 만드는 값이고 극소화시킬 때는 가장 작게 만드는 값입니다). 만약 최적화할 수 있는 값이 여러 개이면 해찾기는 가장 처음에 찾은 값에서 해찾기를 멈춥니다.

Excel Solver 추가 기능을 사용해 본 적이 있다면 옵션이 많고 다소 압도적일 수 있습니다. 여기에서는 Excel에서 올바른 해결 방법을 선택하여 문제에 대한 최적의 솔루션을 효율적으로 찾는 데 도움이 되는 실용적인 정보를 제공하고자 합니다.

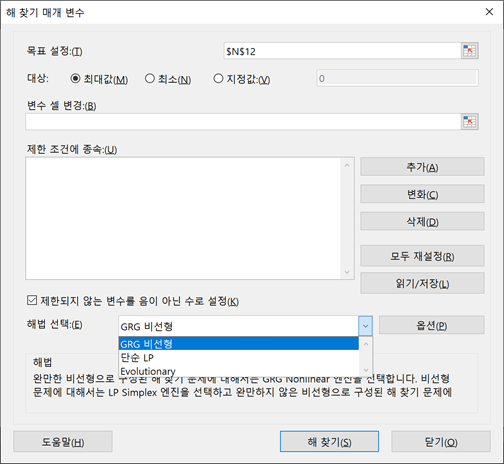
Excel에서 Solver를 설정할 때 선택해야하는 것 중 하나는 “해법 선택(solving method)” 입니다. 선택할 수 있는 세 가지 방법 또는 알고리즘이 있습니다.

• GRG 비선형
• 단순 LP
• Evolutionary

GRG 비선형과 Evolutionary은 비선형 문제에 대해 최적화되어 있으며 단순 LP는 선형문제에만 제한됩니다

GRG는 “Generalized Reduced Gradient”의 약자입니다. 가장 기본적인 형태로, 이 “해법 선택”은 입력 값 (또는 결정 변수) 변화로 목적 함수의 기울기 또는 기울기를 보고 부분 미분 결과가 0 일 때 최적 솔루션에 도달한 것으로 결정합니다.

두 가지 비선형 해법 선택 중 GRG 비선형이 절충하는 방법을 적용하므로 더 빠릅니다.

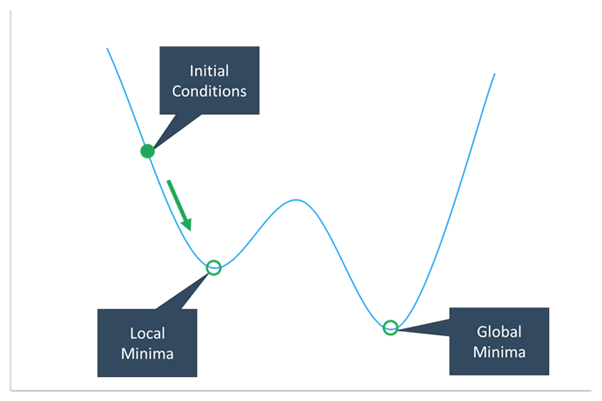
단점은 이 알고리즘으로 얻은 솔루션은 초기 조건에 따라 크게 달라지며 최적의 글로벌 최적값이 아닐 수 있습니다. Solver는 초기 조건에 가장 가까운 로컬 최적값에서 정지하여 글로벌적으로 최적화되거나 아닌 솔루션을 제공할 수 있습니다.

GRG 비선형 Solver가 좋은 결과를 얻기 위해 필요한 또 다른 요구 사항은 함수가 매끄러워야 한다는 것입니다. 예를 들어 IF, VLOOKUP 또는 ABS 함수로 인한 불연속이 발생되면 이 알고리즘에 문제가 발생할 수 있습니다.

Evolutionary 알고리즘은 글로벌하게 최적의 솔루션을 찾을 가능성이 높기 때문에 GRG 비선형보다 강력(robust)합니다. 그러나 이 “해법 선택”은 매우 느립니다.

Evolutionary 방법은 최적의 결과가 사전에 정의되었기 때문에 이러한 경우에는 잘 작동되는 자연 선택 이론에 기초합니다.

간단히 말해서, Solver는 입력값 세트의 임의의 “모집단(population)”로 시작합니다. 이러한 입력값 세트가 모델에 연결되고 결과는 목표 값을 기준으로 평가됩니다.

목표 값에 가장 가까운 솔루션을 제공하는 입력값 세트는 “자손(offspring)”이라는 두 번째 모집단을 생성하도록 선택됩니다. 자손은 첫 번째 모집단 입력값 중에서 최적값 집합의 “변이(mutation)”이라 할 수 있습니다.

그렇게 두번째 모집단도 평가되고, 최선의 값은 세번째 모집단을 창조하도록 선택됩니다.

아래 그림은 좀더 명확하게 이를 설명하고 있습니다.

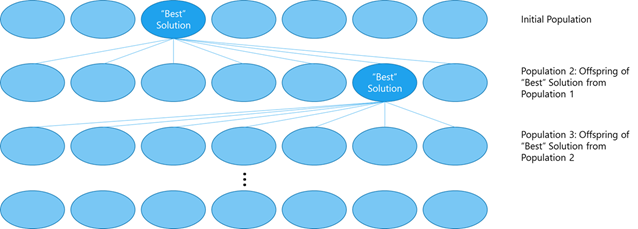
이것은 한 모집담에서 다음 모집단으로 목표값에 대해 거의 변화가 없을 때까지 계속됩니다.

이 과정에 대해 시간이 많이 걸리는 이유는 모집단의 각 구성원을 개별적으로 평가해야 한다는 것입니다. 또한 차후의 “세대(generations)”는 다음 최고의 값의 집합을 찾기 위해 미분이나 목적 함수의 기울기를 사용하는 대신에 임의의 값으로 채워집니다.

이제 Excel에서는 Solver 옵션 창을 통해 알고리즘을 제어할 수 있습니다. 예를 들어, 변이율 및 모집단 크기를 선택하여 솔루션을 잠재적으로 단축할 수 있습니다.

그러나 모집단 크기를 줄이거나 변이율을 증가시키면 수렴에 도달하기에 더 많은 모집단들이 필요할 수 있기 때문에 결과를 약화시킬 수 있습니다.

GRG 비선형 알고리즘의 속도와 Evolutionary 알고리즘의 견고성(robustness) 사이의 좋은 타협점은 GRG 비선형 Multistart 입니다. Solver 옵션을 통해 GRG 비선형 탭 아래의 이 옵션을 활성화할 수 있습니다.

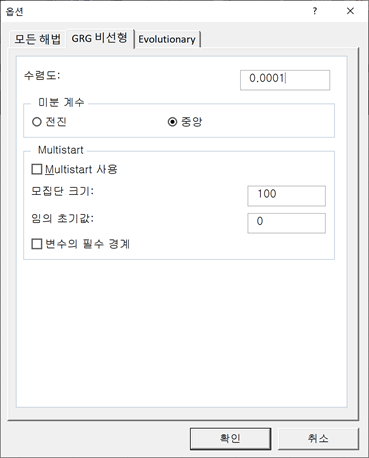
이 알고리즘은 기존의 GRG 비선형 알고리즘을 사용하여 각각 평가되는 초기값에 대한 임의로 분포된 모집단을 생성합니다.

서로 다른 초기 조건에서 여러 번 시작하면 발견되는 솔루션이 글로벌 최적값일 가능성이 훨씬 높아집니다.

세 가지 해결 방법 중 단순 LP를 가장 적게 사용합니다. 선형 함수만 포함된 문제에 적용할 수 있으므로 응용에 제한적입니다.

많은 경우에, 해결하고자 하는 문제는 비선형입니다. 그리고 그것들이 선형일 때는 대신 그것들을 행렬 방정식으로 푸는 것을 더 선호합니다.

그러나 해결하려는 문제가 선형인 경우 단순 LP 방법으로 얻은 솔루션이 항상 글로벌한 최적의 솔루션이라는 것을 확신할 수 있기 때문에 매우 강력(robust)합니다.