(a, b, 0) 클래스 추가학습
건수 분포는 음이 아닌 정수 0,1,2,…의 값을 취하는 이산형 임의의 변수입니다. 예를 들어 포아송 분포, 이항 분포 및 음이항 분포가 있습니다. 이러한 분포는 관심있는 몇몇 임의의 사건에 대한 발생 횟수 – 예를 들어 보험계리적 응용의 손실 건수에 대한 – 잠재적 모델입니다. 아래의 논의는 (a, b, 0) 클래스의 개념이 포아송, 이항 및 음이항의 세 가지 큰 분포를 설명하는 또 다른 방법임을 보여줍니다. (a, b, 1) 클래스의 개념은 (a, b, 0) 클래스의 일반화입니다.
(a, b, 0) 클래스
(a, b, 0) 클래스는 확률을 생성하는 재귀 알고리즘입니다. 몇 가지 표기법을 수정해 봅시다. N은 건수 임의의 변수입니다. 각각 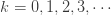 에 대해 Pk = P [N = k] 입니다. 건수 임의의 변수
에 대해 Pk = P [N = k] 입니다. 건수 임의의 변수 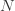 은 어떤 상수
은 어떤 상수  와
와 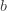 에 대해 다음의 재귀 관계가 유지되는 경우 분포의 (a, b, 0) 클래스의 멤버라고 합니다.
에 대해 다음의 재귀 관계가 유지되는 경우 분포의 (a, b, 0) 클래스의 멤버라고 합니다.

재귀관계 (1)은 1 에서 시작하여 모든 정수 k에 대해 모든 확률 Pk를 생성합니다. 그 관계 (1)은 P0를 고려하지 않습니다. 그것은 초기 확률 P0
이 임의의 확률 값일 수 있다는 것을 의미합니까? 재귀관계 (1)은 각각 Pk가 궁극적으로 P0로 표현됨을 의미합니다.
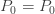
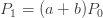
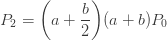
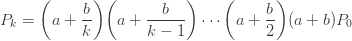
 와
와  의 값이 고정되는 경우, P0 값은 그 확률의 합이 1이 되어야 하므로 역시 고정됩니다. 실제로 P0
의 값이 고정되는 경우, P0 값은 그 확률의 합이 1이 되어야 하므로 역시 고정됩니다. 실제로 P0
는 다음의 값입니다.
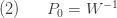
여기서 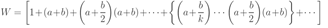
따라서, (a, b, 0) 클래스는 a 및 b라는 분포를 완전히 결정하는 두 개의 모수를 가집니다.
예제 1
예를 들어, a=0 및 b=λ (λ>0인)인 고정된 양의 상수가 있다고 합시다. (1)을 사용하면 다음과 같습니다.
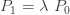

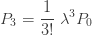
…… .. 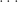
…… .. 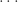
…… .. 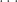
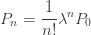
…… .. 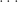
…… .. 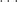
…… ..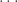
(2)에 따르면 P0 = e-λ
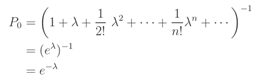
P0 = e-λ 을 사용하면 확률 Pn은 푸아송 분포에서 나옵니다. 따라서 모수 a가 0이고 모수 b가 양의 상수인 경우 (a, b, 0) 클래스의 해당 분포는 포아송 분포입니다.
(a, b, 0) 클래스에서 3가지 맴버
본질적으로 (a, b, 0) 클래스는 크게 3개의 이산 분포, 즉 포아송 분포, 이항 분포 및 음이항 분포와 같은 3 개의 구서원을 가지며 각 분포는 모수 a의 다른 부호로 표시됩니다. 재귀관계 (1)을 사용하면 큰 세가지 분포가 각각 (a, b, 0) 클래스에 속한다는 것을 알 수 있습니다. 다음 표는 세가지 경우에서 모수 a와 b를 보여줍니다.
표 1
| 분포 | 일반적인 모수 | 모수 a | 모수 b |
| 푸 아송 | 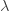 |
0 | 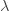 |
| 이항식 | 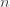 과 과 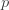 |
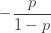 |
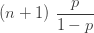 |
| 음이항 |  과 과 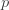 |
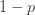 |
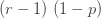 |
| 음이항 |  과 과 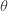 |
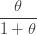 |
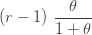 |
| 기하 | 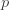 |
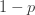 |
0 |
| 기하 | 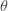 |
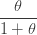 |
0 |
표 1은 세 가지 분포를 모수화하는 방법을 보여줍니다. 예를 들어, 모수 n(시험 횟수) 및 p (성공 확률)가 있는 이항 분포의 경우 (a, b, 0) 모수는 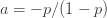 및
및 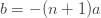 입니다. 음이항에 대한 두번째 행은 두 개의 다른 모수를 반영합니다. 물론, 기하 분포는 모수 r=1일 때 단순히 음이항 분포 입니다. 본질적으로 표 1은 세 가지 다른 분포로 구성됩니다.
입니다. 음이항에 대한 두번째 행은 두 개의 다른 모수를 반영합니다. 물론, 기하 분포는 모수 r=1일 때 단순히 음이항 분포 입니다. 본질적으로 표 1은 세 가지 다른 분포로 구성됩니다.
표 1은 물론 반대 방향으로도 작동합니다. 모수 a와 b를 갖는 (a, b, 0) 세트는 표 1에서 보여준 분포의 하나로 적합되어야 합니다. 다시 말해서 재귀관계 (1)은 개로운 건수 분포를 생성하지 않습니다. (1)을 만족하는 모든 건수 분포는 표1에 나열된 3개의 건수 분포 중 하나여야 합니다.
재귀관계 (1) 하에서 a와 b의 모든 조합이 확률 분포를 만드는 것은 아닙니다 . 예를 들어  및
및 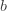 가 모두 음수의 상수인 경우 확률
가 모두 음수의 상수인 경우 확률 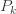 의 결과는
의 결과는 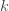 가 홀수에 대해서는 음수입니다. a+b<0 일 때, 확률 Pk의 결과는 이 모든 경우에 확실하게 양수일 수는 없습니다. a+b=0일 때, P0=1입니다. 즉, 분포는 0에서 모든 사건이 발생됩니다. 그러므로 a+b>0 인 경우로 관심을 제한하고자 합니다.
가 홀수에 대해서는 음수입니다. a+b<0 일 때, 확률 Pk의 결과는 이 모든 경우에 확실하게 양수일 수는 없습니다. a+b=0일 때, P0=1입니다. 즉, 분포는 0에서 모든 사건이 발생됩니다. 그러므로 a+b>0 인 경우로 관심을 제한하고자 합니다.
이전에 작성된 점을 반영하기 a+b>0이고 재귀관계 (1)이 실행 가능한 확률 분포를 생성하는 경우, 그 결과적인 분포는 표 1에 나열된 세 가지 분포 중 하나여야 합니다. 이 점은 완전히 명백하지는 않습니다. 관심있는 독자라면 추가 자료를 찾아 보십시요.
표1은 모수 a의 부호가 (a, b, 0) 분포의 형태를 결정함을 나타냅니다. A=0인 경우, 포아송 분포입니다. a가 음수인 경우, 그것은 이항 분포이다. a가 양수인 경우, 그것은 음이항 분포입니다.
예제
이제 (a, b, 0) 재귀 관계의 작동을 설명하는 몇 가지 예제를 더 제시합니다.
예제 2
이 예는 (a, b, 0) 클래스 멤버의 세 가지 연속 확률을 아는 것이 전체 분포를 결정한다는 것을 보여줍니다. 예를 들어,
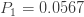
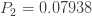
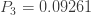
이 세 가지 연속 확률은 다음과 같은 a와 b에 대한 두 개의 선형 방정식을 생산합니다.
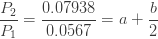
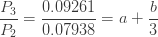
이 두 선형 방정식을 풀면 a=0.7 및 b=1.4가 계산됩니다.  가 양수이므로 음이항 분포입니다. 해당 음이항 모수는 r=3 및 p=0.3입니다. 이 정보를 사용하여 (a, b, 0) 분포가 완전히 결정됩니다. 다음은 몇 가지 분포 통계량입니다.
가 양수이므로 음이항 분포입니다. 해당 음이항 모수는 r=3 및 p=0.3입니다. 이 정보를 사용하여 (a, b, 0) 분포가 완전히 결정됩니다. 다음은 몇 가지 분포 통계량입니다.
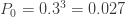
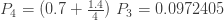
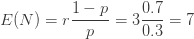
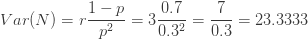
예제 3
실제로 주어진 3개의 확률로 전체 (a, b, 0) 분포가 결정됩니다. 연속될 필요는 없습니다. 다음과 같은 확률이 있다고 가정합니다.
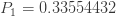
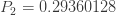
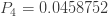
재귀관계 (1)를 적용하면 다음 방정식이 생성됩니다.
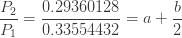
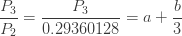
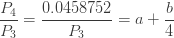
위의 3 가지 방정식은 다음 두 가지 방정식으로 이어집니다.
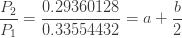
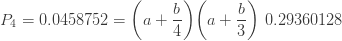
위의 두 방정식 중 하나는 선형 방정식이고 다른 하나는 2차 방정식입니다. 이 두 방정식을 풀면 a=-0.25 및 b=2.25 를 계산합니다.  가 음수이므로 이항 분포입니다. 표 1의 변환을 사용하면 다음 방정식이 제공됩니다.
가 음수이므로 이항 분포입니다. 표 1의 변환을 사용하면 다음 방정식이 제공됩니다.

이 방정식을 풀면 n=8 및 p=0.2가 나타납니다 . (a, b, 0) 분포가 완전히 결정됩니다.
고차원 모멘트(Factorial Moments)
(a, b, 0) 클래스에 대한 통찰력을 제공할 수 있는 또 다른 분포 통계량은 고차원 모멘트입니다. 임의의 변수 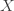 의 경우
의 경우 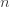 번째 계승 모멘트는
번째 계승 모멘트는
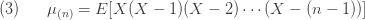
예를 들어, 처음 세 가지 계승 모멘트는 다음과 같습니다.
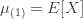
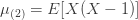
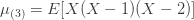
모수 a, b를 가지는 (a, b, 0) 클레스에 대해 첫번째 고차원 모멘트는 다음과 같습니다:
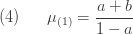
더 높은 (a, b, 0) 계승 모멘트는 다음과 같이 재귀적으로 얻을 수 있습니다.
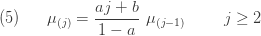
재귀공식 (5)는 (a, b, 0) 클래스 멤버의 원시 모멘트를 결정하는 좋은 방법입니다. 예를 들어, 다음은 모수 a, b를 가지는 (a, b, 0) 클레스의 구성원이 되는 것으로 가정되어지는 임의의 변수 N의 2차 원래 모멘드 및 분산을 계산합니다.
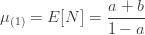
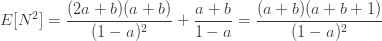
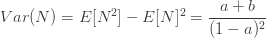
(a, b, 0) 클래스의 흥미로운 특징 중 하나는 제한된 분포 정보를 아는 것이 분포를 결정한다는 것입니다. 예제 2와 예제 3은 3개의 점의 질량을 아는 것이 (a, b, 0) 분포를 완전히 결정한다는 것을 보여줍니다. 위의 유도는 평균과 분산을 아는 것도 (a, b, 0) 분포를 완전히 결정한다는 것을 보여줍니다.
(a, b, 0) 분포의 적합
(1)에서의 (a, b, 0) 재귀공식이 새로운 분포를 생성하지 않는 경우, 왜 (a, b, 0) 클래스를 연구하고 왜 포아송, 이항 및 음이항 분포에 중점을 두지 않는가? 재귀 (a, b, 0) 공식을 연구하는 한 가지 이유는 (a, b, 0) 클래스의 적절한 구성원을 선택하는 그래픽적인 방식을 제공하기 때문입니다. 이것을 보려면 다음과 같이 (1)을 다시 작성하십시오.
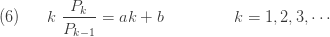
(6)의 오른쪽에 있는 수식은 정수 k에 대한 선형 함수입니다. x 축이 k를 갖는 (6)의 왼쪽 수식을 그림으로 표시하는 경우, 기울기는 모수 a이고 y절편이 모수 b인 선형 그림이어야 합니다. (물론 (a, b, 0) 분포를 가정하는 경우)
관계식 (6)은 주어진 샘플이 (a, b, 0) 클래스의 멤버에서 가져 왔는지 여부를 신속하게 결정하는 방법입니다. 이렇게 하기 위해서는 k번째의 두 연속 데이터 범주의 비율을 계산해야 합니다. 다시 말해, k의 값에 대해 다음과 같은 값에 대한 비율을 계산해야 합니다.
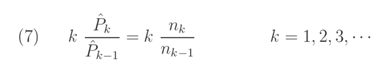
여기서 nk는 k범주에 대한 관찰 빈도입니다. k를 곱한 nk에 대한 nk-1 비율은 (6)의 좌측 수식의 대체 수식입니다. 그런 다음 k값에 대해 플로팅합니다. 그래프에서 관찰되는 선형 추세가 샘플에서 데이터가 (a, b, 0) 분포에서 가져온 증거라 할 수 있습니다.
표시된 선의 기울기는 사용할 (a, b, 0) 구성원을 나타냅니다. 그림이 대략 수평이면 포아송 모형이 적합합니다. 그림이 음의 기울기를 가진 선인 경우 이항 모형이 더 적합합니다. 그림이 대략 양의 기울기가 있는 경우 음이항 모델을 사용하십시오. 이 접근 방식이 제대로 작동하려면 큰 관측 데이터 세트가 선호됩니다.
(a, b, 1) 클래스
(a, b, 0) 분포는 관찰되는 임의의 건수 현상을 적절하게 설명하지 않을 수 있습니다. 예를 들어, 샘플 데이터는 0에서의 확률이 (a, b, 0) 클래스의 분포에 의해 표시된 것보다 크게 나타날 수 있습니다. 한 가지 대안은 P0에 대해 더 큰 값을 할당하고 이후의 확률 Pk (k=2,3,…)를 재귀적으로 생성하는 것 입니다. 이러한 재귀 체계에 의해 정의된 분포 클래스를 (a, b, 1) 클래스라고 합니다.
