(a, b, 1) 클래스 심화학습
(a, b, 1) 클래스
건수 분포는 음이 아닌 정수를 취하는 이산 확률 분포입니다. 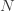 은 건수 분포의 임의의 변수 입니다. 각 정수
은 건수 분포의 임의의 변수 입니다. 각 정수 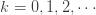 에 대해
에 대해 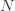 이 고려해야할 건수 분포라고 하면,
이 고려해야할 건수 분포라고 하면, 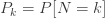 입니다. 다음의 재귀관계가 어떤 상수 a, b를 가지는 경우 건수 분포는 (a, b, 0) 클래스의 분포에 속합니다.
입니다. 다음의 재귀관계가 어떤 상수 a, b를 가지는 경우 건수 분포는 (a, b, 0) 클래스의 분포에 속합니다.


(a, b, 0) 클래스에 속하는 경우 초기 확률 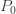 이 고정됩니다 (모든
이 고정됩니다 (모든 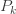 의 합은 반드시 1이 되어야 합니다). 따라서, (a, b, 0) 클래스에 속하는 경우 두 개의 모수, 즉,
의 합은 반드시 1이 되어야 합니다). 따라서, (a, b, 0) 클래스에 속하는 경우 두 개의 모수, 즉,  및
및 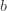 는 재귀 관계 (1)에 있습니다. 다음의 재귀관계가 어떤 상수 a, b를 가지는 경우 건수 분포는 (a, b, 1) 클래스에 속합니다.
는 재귀 관계 (1)에 있습니다. 다음의 재귀관계가 어떤 상수 a, b를 가지는 경우 건수 분포는 (a, b, 1) 클래스에 속합니다.
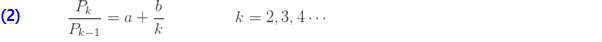
(a, b, 1) 클래스에서 재귀는k=2에서 시작합니다. 즉, 초기 확률 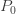 은 가정된 값이어야 합니다. 그러면 확률
은 가정된 값이어야 합니다. 그러면 확률 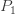 은 합
은 합 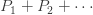 이
이 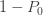 이 되는 값이어야 합니다. 따라서, ( a, b, 1) 클래스에 속하는 경우 세 개의 모수를 갖습니다 :
이 되는 값이어야 합니다. 따라서, ( a, b, 1) 클래스에 속하는 경우 세 개의 모수를 갖습니다 :  ,
, 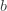 및
및 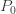 .
.
분포의 (a, b, 1) 클래스에는 두 개의 서브 클래스가 있습니다. 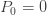 또는
또는 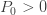 에 따라 결정됩니다. 첫번째 범주에서의 (a, b, 1) 클래스는 제로 절단 분포라고 합니다. 두 번째 범주에서의 (a, b, 1) 분포는 제로 수정 분포라고 합니다.
에 따라 결정됩니다. 첫번째 범주에서의 (a, b, 1) 클래스는 제로 절단 분포라고 합니다. 두 번째 범주에서의 (a, b, 1) 분포는 제로 수정 분포라고 합니다.
(a, b, 0) 클래스에서 시작점으로써의 주어진 분포를 시작점으로 사용하는 경우 제로 절단된 분포를 도출하는 방법을 보여줍니다. 주어진 제로 절단된 분포로부터, 제로 수정된 분포를 도출하는 방법을 보여줍니다.
(a, b, 1) 분포의 이름은 접두사가 제로 절단 또는 제도 수정 이라는 이름을 가지는 동일한 (a, b, 0) 이름을 갖습니다. 예를 들어, 시작점이 (a, b, 0) 클래스에서 음이항 분포인 경우 (a, b, 1) 클래스의 파생 분포는 제로 절단 음이항 분포와 제로 수정 음이항 분포입니다.
(a, b, 0) 클래스에는 포아송, 이항 및 음이항의 세 가지 분포만 있습니다. 그런 다음 (a, b, 1) 클래스에는 이 세 가지 분포의 제로 절단 및 제로 수정 버전을 포함합니다. 그러나 (a, b, 1) 클래스는 (a, b, 0) 분포에서 수정되지 않은 분포를 포함합니다. ETNB (Extended Tuncated Negative Binomial) 분포, 대수(logarithmic) 분포 및 시부야(Sibuya) 분포 등 세 가지 추가 분포에 대해 설명합니다. (a, b, 0) 분포에서 파생되지 않은 이 세 분포들은 아래의 별도 섹션에서 설명합니다.
우리는 기본적인 (a, b, 0) 음이항 분포를 사용하여 제로 절단 음이항 분포(예제 1) 및 제로 수정 음이항 분포(예제 2)를 도출하는 방법을 보여주는 세 가지 예를 제시합니다. 또한 ETNB 분포에 대한 예제를 제공합니다 (예제 3).
표기법
토론을 용이하게 하기 위해 몇 가지 표기법을 수정해 봅시다. 분포를 명확하게 나타내기 위해 위첨자와 첨자가 없는 표기법은 (a, b, 0) 분포를 나타냅니다. 위첨자 T (또는 아래 첨자 T)가있는 표기법은 (a, b, 1) 클래스에서 제로 절단 분포를 나타냅니다. 마찬가지로 위첨자 M (또는 아래 첨자 M)을 사용한 표기법은 (a, b, 1) 클래스에서 제로 수정 분포를 나타냅니다.
예를 들어, 다음은 (a, b, 0) 클래스의 분포에 대한 확률 함수(pf) 및 확률 생성 함수 (pgf)입니다.

다음은 (a, b, 1) 클래스에서 제로 절단 분포에 대한 pf 및 pgf 표기법을 보여줍니다.

다음은 (a, b, 1) 클래스의 제로 수정 분포에 대한 pf 및 pgf 표기법을 보여줍니다.

그렇게 하는 것이 편리할 때마다, 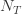 과
과 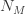 가 각각 제로 절단 분포 및 제로 수정 분포에 대한 임의의 변수를 의미하는 경우,
가 각각 제로 절단 분포 및 제로 수정 분포에 대한 임의의 변수를 의미하는 경우, 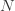 은 (a, b, 0)에서 임의의 변수 입니다.
은 (a, b, 0)에서 임의의 변수 입니다.
제로 절단 분포
이 섹션의 초점은 (a, b, 0) 클래스에서 시작된 제로 절단 분포에 중점을 둡니다. 위에 표시된 세 가지 분포 (ETNB, 로그 및 시부야)는 아래의 별도 섹션에서 설명합니다.
우리는 위에서 설명한 바와 같이 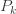 ,
, 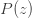 그리고
그리고 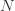 표기법로부터 분포 (a, b, 0) 클래스에서 시작한다고 가정해 봅시다. (a, b, 1) 클래스에서 해당되는 제로 절단 분포를 도출하는 방법을 보여줍니다. 제로 절단 분포의 경우 확률을 계산하는 두 가지 방법이 있습니다. 그중 하나는 재귀관계입니다.
표기법로부터 분포 (a, b, 0) 클래스에서 시작한다고 가정해 봅시다. (a, b, 1) 클래스에서 해당되는 제로 절단 분포를 도출하는 방법을 보여줍니다. 제로 절단 분포의 경우 확률을 계산하는 두 가지 방법이 있습니다. 그중 하나는 재귀관계입니다.
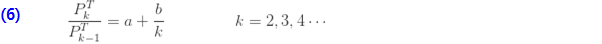
재귀관계(6)는 (2)와 동일합니다. 재귀는 k=2에서 시작합니다. 제로 절단 확률은 다음과 같이 (a, b, 0) 확률에서 파생될 수도 있습니다.
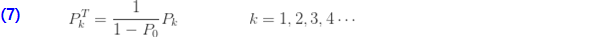
(7)에 있는 확률 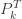 확률의 조건부 확률로 간주될 수 있습니다. 즉 N>0 으로 주어진
확률의 조건부 확률로 간주될 수 있습니다. 즉 N>0 으로 주어진 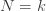 인 확률. 절차적인 관점에서, 확률
인 확률. 절차적인 관점에서, 확률 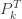 은 (a, b, 0) 확률에
은 (a, b, 0) 확률에 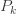 에
에 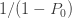 확률을 곱하여 합이 1이 되게 만듭니다. 확률이 설정되면 확률 생성 함수(pgf)와 제로 절단 분포의 평균과 모멘트는 또한 (a, b, 0) 분포의 해당 수식으로 표현됩니다.
확률을 곱하여 합이 1이 되게 만듭니다. 확률이 설정되면 확률 생성 함수(pgf)와 제로 절단 분포의 평균과 모멘트는 또한 (a, b, 0) 분포의 해당 수식으로 표현됩니다.
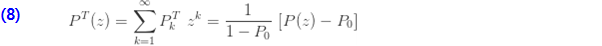


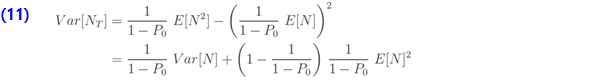
위 수식의 목표는 (a, b, 0) 분포의 정보를 기반으로 제로 절단 분포를 나타내는 것입니다. 확률 함수(7)를 사용한 정의를 기반으로 도출할 수도 있습니다. 다음은 제로 절단 분포의 계승(factorial) 평균을 보여줍니다.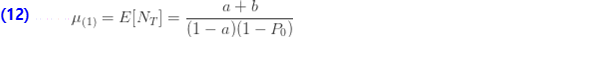 …… ..
…… ..
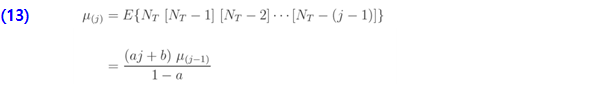
첫 번째 계승 평균은 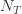 의 평균과 같습니다.
의 평균과 같습니다. 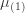 에서
에서 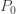 은 (a, b, 0) 클레스에 대응하는 0인 확률의 값입니다. 더 높은 계승 모멘트는 (a, b, 0) 경우에서와 같이 재귀적으로 도출됩니다. 원래 모멘트
은 (a, b, 0) 클레스에 대응하는 0인 확률의 값입니다. 더 높은 계승 모멘트는 (a, b, 0) 경우에서와 같이 재귀적으로 도출됩니다. 원래 모멘트 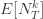 는 계승 모멘트를 사용하여 도출할 수 있습니다. 계승 모멘트에서 파생된 분산은 다음과 같습니다.
는 계승 모멘트를 사용하여 도출할 수 있습니다. 계승 모멘트에서 파생된 분산은 다음과 같습니다.
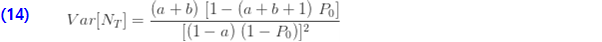
예제 1
예제를 살펴 보는 것이 도움이 됩니다. 먼저, (a, b, 0) 분포–모수 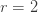 와
와 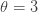 을 갖는 음이항 분포를 설정합니다. (a, b, 0) 모수는
을 갖는 음이항 분포를 설정합니다. (a, b, 0) 모수는 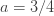 및
및 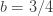 입니다. 다음은 이 음이항 분포에 대한 pf와 재귀관계, 평균, 분산 및 pgf를 보여줍니다.
입니다. 다음은 이 음이항 분포에 대한 pf와 재귀관계, 평균, 분산 및 pgf를 보여줍니다.
…… ..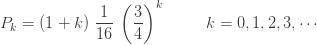
…… ..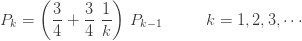
…… ..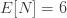
…… ..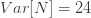
…… ..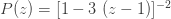
다음 표는 자르지 않은 음이항 분포의 처음 5개의 확률을 보여줍니다.
표 – 제로 절단된 음이항
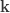 |
(a, b, 0) 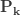 |
제로 절단된 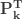 |
|
| 0 | 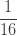 |
||
| 1 | 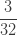 |
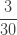 |
|
| 2 | 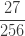 |
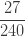 |
|
| 삼 | 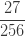 |
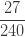 |
|
| 4 | 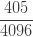 |
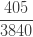 |
|
| 5 | 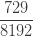 |
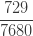 |
|
확률 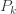 은 (a, b, 0)의 pf 또는 재귀관계에 의해 생성됩니다. 확률
은 (a, b, 0)의 pf 또는 재귀관계에 의해 생성됩니다. 확률 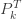 는 재귀관계 (7) 또는 재귀관계 (6)에 의해 생성됩니다. 다음은 제로 절단 음이항 예제의 평균, 분산 및 pgf를 나열합니다.
는 재귀관계 (7) 또는 재귀관계 (6)에 의해 생성됩니다. 다음은 제로 절단 음이항 예제의 평균, 분산 및 pgf를 나열합니다.
…… ..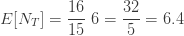
…… ..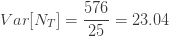
…… ..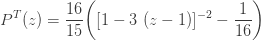
제로 수정 분포
이 섹션의 목표는 이전 섹션에서 설명한대로 (a, b, 0) 분포에서 파생되었거나 (a, b, 0) 분포에서 파생되지 않은 절단된 분포인 제로 절단 분포로부터 제로 수정 분포를 도출하는 것입니다.
이제 주어진 제로 절단 분포를 취하고 확률 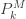 과 다른 분포 계량 내용을 도출합니다. 제로 절단 분포의 경우와 같이 확률을 생성하는 한 가지 방법은 재귀 프로세스를 사용하는 것입니다.
과 다른 분포 계량 내용을 도출합니다. 제로 절단 분포의 경우와 같이 확률을 생성하는 한 가지 방법은 재귀 프로세스를 사용하는 것입니다.
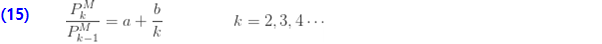
확률 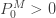 은 가정된 값입니다. 확률
은 가정된 값입니다. 확률 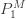 은 모든 확률의 합이 1이 되도록 하는 값입니다. 표시된 대로 재귀는 k=2에서 시작합니다. 확률을 계산하는 또 다른 방법은 제로 절단된 분포를 이용하는 것입니다.
은 모든 확률의 합이 1이 되도록 하는 값입니다. 표시된 대로 재귀는 k=2에서 시작합니다. 확률을 계산하는 또 다른 방법은 제로 절단된 분포를 이용하는 것입니다.
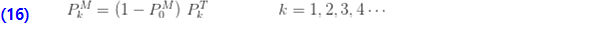
물론 제로 절단 분포가 (a, b, 0) 클래스의 분포를 기반으로 하는 경우 (7)을 (16)에 대입한 후 다음과 같이 제로 수정 확률로 표현할 수 있습니다.
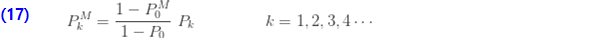
추가 분포 수량을 이제 도출 할 수 있습니다.
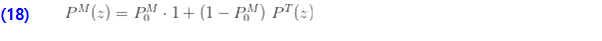

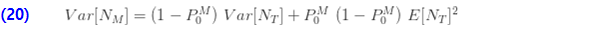
결과 (18)은 주어진 제로 절단 분포의 pgf를 기준으로 제로 수정 분포의 pgf입니다. 다시 말해, (19)는 수정 분포의 평균이 주어진 제로 절단 분포의 평균에 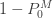 을 곱한 갓이라고 말할 수 있습니다. 또한, (20)은 제로 수정 분포의 분산은 주어진 제로 절단 분포의 분산에
을 곱한 갓이라고 말할 수 있습니다. 또한, (20)은 제로 수정 분포의 분산은 주어진 제로 절단 분포의 분산에 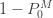 배를 하고 절단 분포의 평균을 제곱하여
배를 하고 절단 분포의 평균을 제곱하여 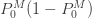 배 한 값을 곱한 것입니다.
배 한 값을 곱한 것입니다.
주어진 제로 절단 분포가 실제로 (a, b, 0) 클래스에서 얻은 경우, 위의 세 가지 결과는 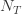 의 대응하는 정보를 (18), (19) 및 (20)으로 변환하 후에 (a, b, 0) 정보로 표현할 수 있습니다.
의 대응하는 정보를 (18), (19) 및 (20)으로 변환하 후에 (a, b, 0) 정보로 표현할 수 있습니다.
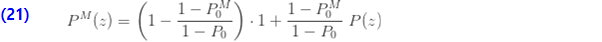

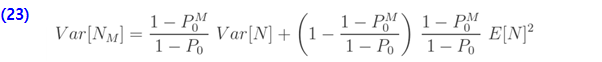
예제 2
예제 1에서 고려된 제로 절단 음이항 분포를 고려해 봅시다. 이제는 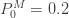 의 가정된 값으로 해당 제로 수정 음이항 분포에 대한 정보를 생성합니다. 다음 표는 몇 가지 확률을 제공합니다.
의 가정된 값으로 해당 제로 수정 음이항 분포에 대한 정보를 생성합니다. 다음 표는 몇 가지 확률을 제공합니다.
표 – 제로 수정 음 이항
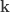 |
(a, b, 0) 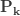 |
제로 절단된 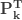 |
제로 수정된 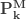 |
|
| 0 | 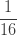 |
0.2 | ||
| 1 | 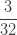 |
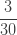 |
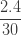 |
|
| 2 | 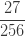 |
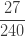 |
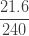 |
|
| 삼 | 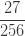 |
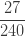 |
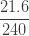 |
|
| 4 | 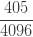 |
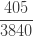 |
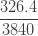 |
|
| 5 | 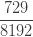 |
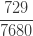 |
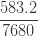 |
|
제로 수정 확률 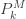 은 (16)에 따라 계산됩니다. 가정된 값
은 (16)에 따라 계산됩니다. 가정된 값 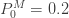 을 가지고
을 가지고 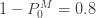 을 산출합니다. 단순히 각각의 제로 절단 확률에 0.8을 곱합니다. (18), (19) 및 (20)을 사용하여, 제로 수정 음이항 예제의 평균, 분산 및 pgf를 구합니다.
을 산출합니다. 단순히 각각의 제로 절단 확률에 0.8을 곱합니다. (18), (19) 및 (20)을 사용하여, 제로 수정 음이항 예제의 평균, 분산 및 pgf를 구합니다.
…… ..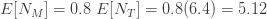
…… ..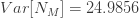
…… ..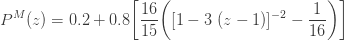
추가적인 제로 절단 분포
앞에서 설명한 것처럼, (a, b, 1) 클래스는 세 개의 (a, b, 0) 분포에서 파생된 것 이외의 분포를 포함합니다. 이 분포들에는 제로 수정된 버전 뿐만 아니라 제로 절단 버전도 있습니다. 절단된 버전에 대해 설명합니다. 확장 절단 음이항 분포(ETNB), 대수 분포 및 시부야 분포가 있습니다. 연장 절단 음이항 분포(ETNB)는 음이항 분포의 r 파라미터를 완화함으로써 발생합니다. 로그 분포와 시부야 분포는 ETNB 분포에서 파생됩니다. 이 세 가지 분포들의 수정된 버전은 이전 섹션에 요약된 프로세스를 통해 얻을 수 있습니다.
ETNB
(a, b, 0) 음이항 분포에는 두 개의 모수  과
과 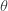 가 있습니다. 다음은 (a, b,0) 재귀 및 처음 두 확률에 사용되는 모수
가 있습니다. 다음은 (a, b,0) 재귀 및 처음 두 확률에 사용되는 모수  와
와 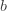 가 주어집니다. ..
가 주어집니다. ..
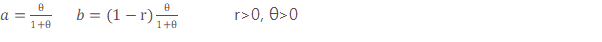
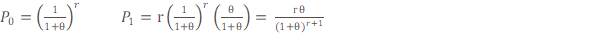
확장된 음이항 분포는 모수 r을 확장함으로써 결과를 얻을 수 있으므로 일반적인 r>0 에 더해서 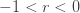 이 적용할 수 있습니다 .r의 확장으로 인해 ETNB 확률은 (7)의 잘린 확률에 따라 생성됩니다. 실제로, 기본적인 (a, b, 0) 음이항 분포에서 시작하는 것처럼 모수 r 조차도
이 적용할 수 있습니다 .r의 확장으로 인해 ETNB 확률은 (7)의 잘린 확률에 따라 생성됩니다. 실제로, 기본적인 (a, b, 0) 음이항 분포에서 시작하는 것처럼 모수 r 조차도 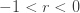 와 같이 될 수 있습니다. 따라서 제로 절단 ETNB 분포의 두 모수는 다음과 같습니다.
와 같이 될 수 있습니다. 따라서 제로 절단 ETNB 분포의 두 모수는 다음과 같습니다.
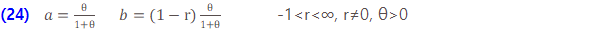
(24)에 표시된 ETNB 모수로 무엇을 합니까? 이 a와 b를 사용하여 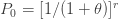 를 가지는 재귀관계 (1)에 따라 “음이항” 확률
를 가지는 재귀관계 (1)에 따라 “음이항” 확률 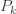 를 생성할 수 있습니다. 그러나 r이 음수이면 이러한 값
를 생성할 수 있습니다. 그러나 r이 음수이면 이러한 값 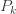 은 확률이 아닙니다(사실 음수 임). 그러나r 이 음이면,
은 확률이 아닙니다(사실 음수 임). 그러나r 이 음이면, 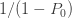 의 값도 음수입니다. (7)을 사용하면, 제로 절단 확률
의 값도 음수입니다. (7)을 사용하면, 제로 절단 확률 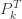 는 양수입니다. 따라서 음수 r을 사용한 “음이항” 분포 는 실제로 분포가 아니고 ETNB 분포를 정의하는 장치 일뿐입니다.
는 양수입니다. 따라서 음수 r을 사용한 “음이항” 분포 는 실제로 분포가 아니고 ETNB 분포를 정의하는 장치 일뿐입니다.
앞 단락의 아이디어를 사용하여 ETNB 확률 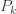 에 대한 직접적인 공식을 도출할 수도 있습니다. 다음은 처음 세 가지 확률을 제공합니다.
에 대한 직접적인 공식을 도출할 수도 있습니다. 다음은 처음 세 가지 확률을 제공합니다.
…… .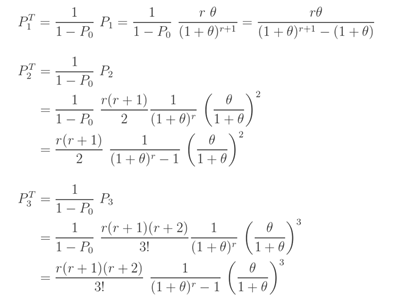
상기 세 확률의 확률 ENTB의 패턴에 기초하여 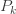 ,
, 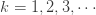 는 다음과 같습니다:
는 다음과 같습니다:
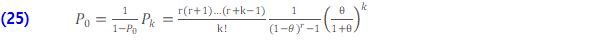
pgf 및 평균 및 더 높은 모멘트와 같은 다른 모든 분포 통계량은 ETNB pf 인 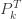 를 기반으로 도출 될 수 있습니다. 예를 들오 평균, 분산 및 pgf는 다음과 같습니다.
를 기반으로 도출 될 수 있습니다. 예를 들오 평균, 분산 및 pgf는 다음과 같습니다.
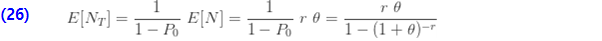
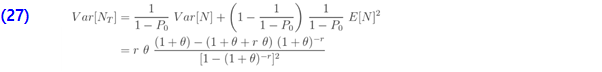
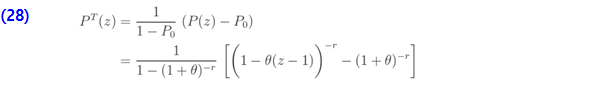
대수 분포
이것은 ETNB에서 r → 0으로 보내므로써 파생된 절단 분포입니다. 다음은 확률의 재귀 생성에 필요한 정보를 보여줍니다.


모수 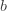 는 ETNB에 대한 b에 대해
는 ETNB에 대한 b에 대해 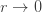 함으로써 얻을 수 있습니다. 로그
함으로써 얻을 수 있습니다. 로그 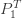 는 ETNB
는 ETNB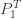 의 극한인
의 극한인 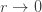 (L’ Hopital의 규칙을 사용하여)함으로써 얻을 수 있습니다.
(L’ Hopital의 규칙을 사용하여)함으로써 얻을 수 있습니다. 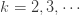 에 대한
에 대한 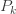 의 나머지는 재귀관계 (6)로부터 생성될 수 있습니다. (a, b, 0) 분포에서 파생된 제로 절단된 분포와 달리 로그 분포의 분포량은 (a, b, 0) 분포에서 도출할 수 없습니다. 따라서 대수에 대한 자세한 정보를 얻으려면 pf를 반드시 사용해야 합니다. 로그 분포의 평균과 분산은 다음과 같습니다.
의 나머지는 재귀관계 (6)로부터 생성될 수 있습니다. (a, b, 0) 분포에서 파생된 제로 절단된 분포와 달리 로그 분포의 분포량은 (a, b, 0) 분포에서 도출할 수 없습니다. 따라서 대수에 대한 자세한 정보를 얻으려면 pf를 반드시 사용해야 합니다. 로그 분포의 평균과 분산은 다음과 같습니다.

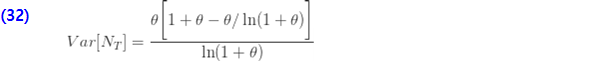
시부야 분포
이것은 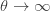 를 보내고
를 보내고 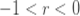 으로 만들므로써 ETNB에서 파생된 절단 분포입니다. 다음은 확률의 재귀적 생성에 필요한 정보를 보여줍니다.
으로 만들므로써 ETNB에서 파생된 절단 분포입니다. 다음은 확률의 재귀적 생성에 필요한 정보를 보여줍니다.


3개의 항목 모두 ETNB의 해당 항목에 대해 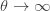 로 보냄으로써 얻습니다.
로 보냄으로써 얻습니다. 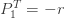 가 됨을 확인하려면 다음과 같이 ETNB인
가 됨을 확인하려면 다음과 같이 ETNB인 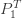 를 다시 작성합니다.
를 다시 작성합니다.
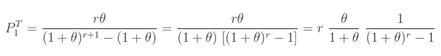
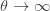 가 됨에 따라, 비율
가 됨에 따라, 비율 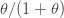 는 1로 갑니다.
는 1로 갑니다. 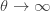 가 됨에 따라, r이 음수가 되므로
가 됨에 따라, r이 음수가 되므로 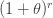 은 0이 됩니다. 따라서 위의
은 0이 됩니다. 따라서 위의 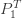 는 =r로 갑니다. (34)의 a와 b와 (35)의
는 =r로 갑니다. (34)의 a와 b와 (35)의 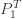 에 대해, 시부야PF의 나머지 부분은 (6)의 재귀관계에 의해 생성될 수 있습니다. 시부야 분포에는 평균이 존재하지 않는 것을 주목하십시요. 다음은 시부야 분포의 pgf입니다.
에 대해, 시부야PF의 나머지 부분은 (6)의 재귀관계에 의해 생성될 수 있습니다. 시부야 분포에는 평균이 존재하지 않는 것을 주목하십시요. 다음은 시부야 분포의 pgf입니다.

이 세 개의 제로 절단 분포가 얻어지면, 앞에서 설명한 프로세스에서 이러한 분포의 제로 수정된 버전을 도출할 수 있습니다.
예제 3
ETNB 계산 방법을 보여줍니다. 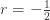 및
및 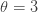 이라고 가정합니다. 그런 다음 “인공적인” 음이항 분포에 대한 모수는 다음과 같습니다.
이라고 가정합니다. 그런 다음 “인공적인” 음이항 분포에 대한 모수는 다음과 같습니다.
…… ..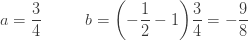
인공적인 음이항 분포에 대한 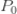 가
가 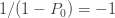 을 만드는
을 만드는 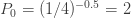 입니다. a와 b를 사용하여 재귀적으로 가짜의 음이항 분포를 생성합니다. 그런 다음 (7)에 따라 제로 절단된 확률을 얻기 위해
입니다. a와 b를 사용하여 재귀적으로 가짜의 음이항 분포를 생성합니다. 그런 다음 (7)에 따라 제로 절단된 확률을 얻기 위해 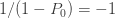 을 곱합니다.
을 곱합니다.
표 – 제로 절단 ETNB
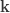 |
인공적인 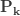 |
제로 절단 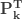 |
|
| 0 | 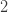 |
||
| 1 | 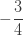 |
 |
|
| 2 | 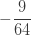 |
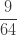 |
|
| 삼 | 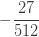 |
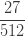 |
|
| 4 | 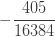 |
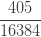 |
|
| 5 | 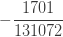 |
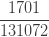 |
|
인공적인 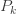 으로 표시된 열은 분명히 확률이 아닙니다.
으로 표시된 열은 분명히 확률이 아닙니다. 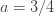 이고
이고 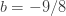 를 사용하여 재귀적으로 생성합니다. 그런 다음 (25)를 직접적으로 사용하여 계산할 수 있는 ETNB 확률을 얻기 위해서 인공적인
를 사용하여 재귀적으로 생성합니다. 그런 다음 (25)를 직접적으로 사용하여 계산할 수 있는 ETNB 확률을 얻기 위해서 인공적인 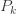 으로 표시된 열에
으로 표시된 열에 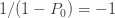 를 곱합니다.
를 곱합니다.
(26) 및 (27)을 사용하여 ETNB 평균 및 분산은 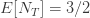 및
및 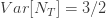 입니다. 가정 된 값은
입니다. 가정 된 값은 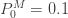 이므로, 다음 표에서 처음 5 개의 제로 수정된 ETNB 확률을 생성합니다.
이므로, 다음 표에서 처음 5 개의 제로 수정된 ETNB 확률을 생성합니다.
표 – 제로 수정 ETNB
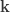 |
인공적인 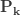 |
제로 절단 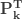 |
제로 수정 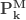 |
| 0 | 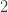 |
0.1 | |
| 1 | 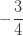 |
 |
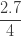 |
| 2 | 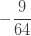 |
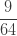 |
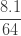 |
| 삼 | 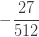 |
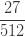 |
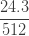 |
| 4 | 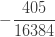 |
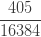 |
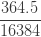 |
| 5 | 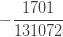 |
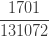 |
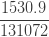 |
가정된 값 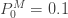 에 대해, 제로 수정 확률은 제로 절단된 확률에
에 대해, 제로 수정 확률은 제로 절단된 확률에 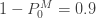 을 곱하여 구합니다 . (19) 및 (20)을 사용하여 제로 수정된 ETNB의 평균 및 분산은
을 곱하여 구합니다 . (19) 및 (20)을 사용하여 제로 수정된 ETNB의 평균 및 분산은 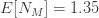 과
과 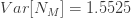 입니다.
입니다.
